当今的智能时代,计算如空气一般,在我们的生活中无处不在。每一条消息发送、每一次网络购物,背后都有很多次的计算在发生,今天人类每秒的计算次数,超过了计算机发明前的人类计算总次数。
然而如何理解计算,是另一个层面的事情。计算的本质是什么,计算可以用来解决什么问题?计算的边界在哪里,什么问题是不可计算的?要如何执行计算,才能更加快速高效?计算的模式,对我们的人生又有怎样的借鉴和指引?
道哥耗时三年写就的这本《计算》,对计算之道,做出了抽丝剥茧的精彩论述,值得反复阅读,常读常新。
本文是阅读《计算》过程中的摘要笔记,试图提炼出书中的核心内容。同时夹杂了一些个人的零散思考(以[PS]前缀标出),这部分没有经过严谨的推理和论证,仅作抛砖引玉。
导论
计算的原理是什么?
这是一切问题的根源,要回答这个问题,就要回顾计算的起源,从数学和哲学层面剖析计算。
毕达哥拉斯的困惑
毕达哥拉斯学派观察到不同事物中蕴含的共同的数学规律,因此认为万物都是由数组成的,这可以被视作计算主义的萌芽。
毕达哥拉斯学派最了不起的地方,在于从一般的特例走向了数学归纳,超越了经验主义而去洞察背后的原理,从公式计算的方法,进化到了公理化和演绎推理的方法,这一研究方法,为后来数学的发展进步奠定了基础。
勾股定理,同时也带来了无理数,由此引发了第一次数学危机。由于毕达哥拉斯学派认为万物皆数,追求事物的和谐,任何量都可以看成两个整数之比,而 这样的无理数,无法表达成整数之比,这种不和谐是毕达哥拉斯学派无法理解和接受的,应对的方式是将发现无理数的希帕索斯,绑起来投入了大海。

演绎推理:逻辑学和几何学
逻辑学
什么是逻辑呢?这要回到逻辑学的诞生之初,亚里士多德对逻辑学的发展做出了巨大的贡献,提出了一个完整的系统性的逻辑推理体系,即三段论,包含大前提、小前提和结论3个部分的论证。比如:
- 大前提:所有的人都会死。
- 小前提:苏格拉底是人。
- 结论:所以苏格拉底会死。
三段论的有效性,依赖于前提是真实的,前提又会有前提,那么最初源头命题的真实性,又该如何证明呢。亚里士多德引入了公理化方法,公理的内容作为逻辑推理的起点,其正确性是不言自明的。
对于人的思维规律,亚里士多德提出了归谬率、排中率和同一律:
- 归谬率:假设某一命题为真,然后推导得出与该命题矛盾、或者明显荒谬的结论,从而证明原命题为假。
- 排中律:同一思维过程中,两个互相矛盾的思想,必有一真,不能同时否定两者。
- 同一律:同一思维过程中,每一思想(概念、判断)必须保持自身的确定性。
基于三段论、公理化方法、逻辑三定律,亚里士多德建立了史上第一个形式逻辑系统。逻辑是人类沟通的基础共识,讲道理,而非胡搅蛮缠,才能有效沟通。
几何学
欧几里得的《几何原本》,是几何学最重要的开山之作,这部书收录了古希腊的所有几何学成就,并继承了亚里士多德的公理化演绎方法,对几何命题加一证明。
欧式几何建立在5条公设和5条公理之上。基于这些公理和公设,《几何原本》全书循序渐进地证明了465个命题,精彩绝伦,公认是最早利用公理化方法建立演绎数学体系的典范。
计算之术
符号与代数
古印度和古代中国的数学,注重经验积累和使用价值,古希腊的数学建立在公理化逻辑推理体系之上,更容易演进发展。
数学符号的提出,通过高效的抽象,剥离了冗余信息,提升了信息的传输效率,使得数学家们,可以使用一致的数学语言,高效沟通。进一步推动了数学的发展。
复数的发现
在探索一元三次方程的一般性解法时,人们遇到了对负数开平方的场景,这超出了当时人们在数论和几何领域的理解,大家无法说清楚对负数开平方的意义,笛卡尔对此结果称为虚数。
后来韦塞尔、高斯成功的将虚数和二维坐标轴联系起来,让其在几何上有了明确的意义,不再是虚无缥缈无法理解的概念,于是虚数被正式命名为复数。复数被诠释为平面内的一个点,复数的加法和乘法,可以表示为平面上线段的向量运算。
复数的出现,让数升级到了二维。那么是否可以继续升维呢?答案是肯定的,但是在升维过程中,我们视为公理的部分运算定律失效了。四元数代数中,乘法交换律失效了,八元数代数中,乘法结合律失效了。人们突然开始意识到,被视作亘古不变的公理,不一定是真理,而只是人为定义。
如果代数方程的系数是有理数,那么求解出来的根则称为代数数。数学家研究发现,一些数不是任何整系数多项式方程的根,他们被称为超越数,比如自然对数底e就是一个超越数。不是多项式方程的根,一定程度上意味着这些数是不可计算的,我们无法在有穷步骤内定义这些数的求解算法。
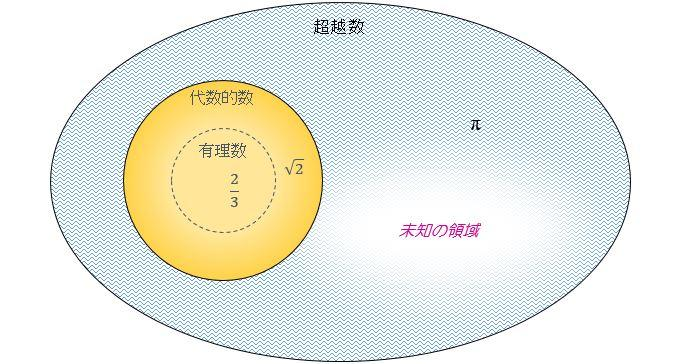
代数的结构
计算可以看作从一些数推导出另一些数的过程,算法则是推导的路径,计算,可以让万物内在的结构显现。
数据家费拉里发现了一元四次方程的求根公式之后,人们开始尝试挑战一元五次方程的代数解。遗憾的是,这一泥潭困扰了人们长达160多年之久。
正向思考碰壁的时候,可以尝试反向思考,如果一直无法找到一元五次方程的代数解,是否有办法证明一元五次方程,不存在代数解呢?基于方程的根和系数之间的关系、根与根之间的关系,鲁菲尼、阿贝尔最终证明了一元五次方程没有通用的代数解。
下一个问题,是一元五次方程,在什么情况下有解呢?
这个问题,要求对系数和方程的关系,有更加深刻和本质的洞察。最终数学家伽瓦罗,通过提出群论,用全新的语言和理论,给出了”多项式方程在什么条件下有根式解“的明确答案,同时开启了抽象代数领域。
抽象代数的诞生,让计算得到了升华。数学家们发现计算不是仅能作用于数,对于一些抽象的数学对象比如群、环、域,计算依然适用,只不过有不同的计算法则。
伽瓦罗的结论,告诉我们什么情况下方程有解,但是很多时候,即使知道解存在,我们也列不出具体的算法,无法计算出精确值,只能退而求其次,寻求近似的数值。这其实已经在暗示着”不可计算问题”的存在。
莱布尼茨的计算之梦
17世纪,莱布尼茨开创了数理逻辑,奠定了现代计算机的基础。核心思想是普遍语言和逻辑计算。
在莱布尼茨的计算之梦中,他期望通过一些字符或符号表达全部思想(普遍语言),使用一种推演计算得到想要的结果(逻辑演算)。
莱布尼茨天才的地方在于,开创性地用数学方法来处理逻辑,提出了逻辑演算和普遍符号的想法,希望设计一套符号,用符号之间的演算来断定真理。当有人发生纠纷时,只需要“算一算“就能做出裁决。

19世纪,英国人乔治布尔首次融合了逻辑和代数,进而创造出了布尔代数,布尔代数是今天计算的重要的理论基础之一。布尔引入了二进制,来驱动逻辑的表达,它大大简化了逻辑推理中需要人工理解的部分,从而可以在计算环节中去除大量人工工作,极大地加快了逻辑推理的速度。
计算的数学基础
第二次数学危机
17世纪,牛顿和莱布尼茨分别独立发明了微积分,但都没有对其依赖的无穷小这一概念,做出明确的阐释。
贝克莱提出了“无穷小量到底是不是0”的悖论,导致了第二次数学危机。
为了驯服无穷小量这一怪兽,柯西首先精确定义了极限和收敛的概念,建立了极限理论。
然而柯西的极限理论并没有定义无理数,以无理数为极限的无穷序列缺少真正的极限。直到19世纪末,这一缺陷才由魏尔斯特拉斯、戴德金和康托尔弥补,精确定义了无理数,这个过程中康托尔创建了集合论。
集合论的诞生
康托尔在研究无穷集合的性质时,运用了一个非常重要的原则:一一对应。当两个集合中的元素一一对应时,则可以认为两个集合中的元素是一样多的。在无穷集合的场景,基于一一对应原则,出现了很多不符合直觉的现象:
- 自然数和自然数的平方一样多
假设自然数的集合为M,自然数的平方集合为N。M中的每一个数,都可以在N中找到对应的数,N中的每个数,也可以在M中找到对应的数,集合M和N是一一对应的。 - 正整数与正有理数一样多
假设正整数的集合为M,正有理数的集合为N。显然M中的每个数,都可以在N中找到对应的数据,对于集合N的有理数,康托尔用一种非常简单的构造方法证明了一一对应关系。
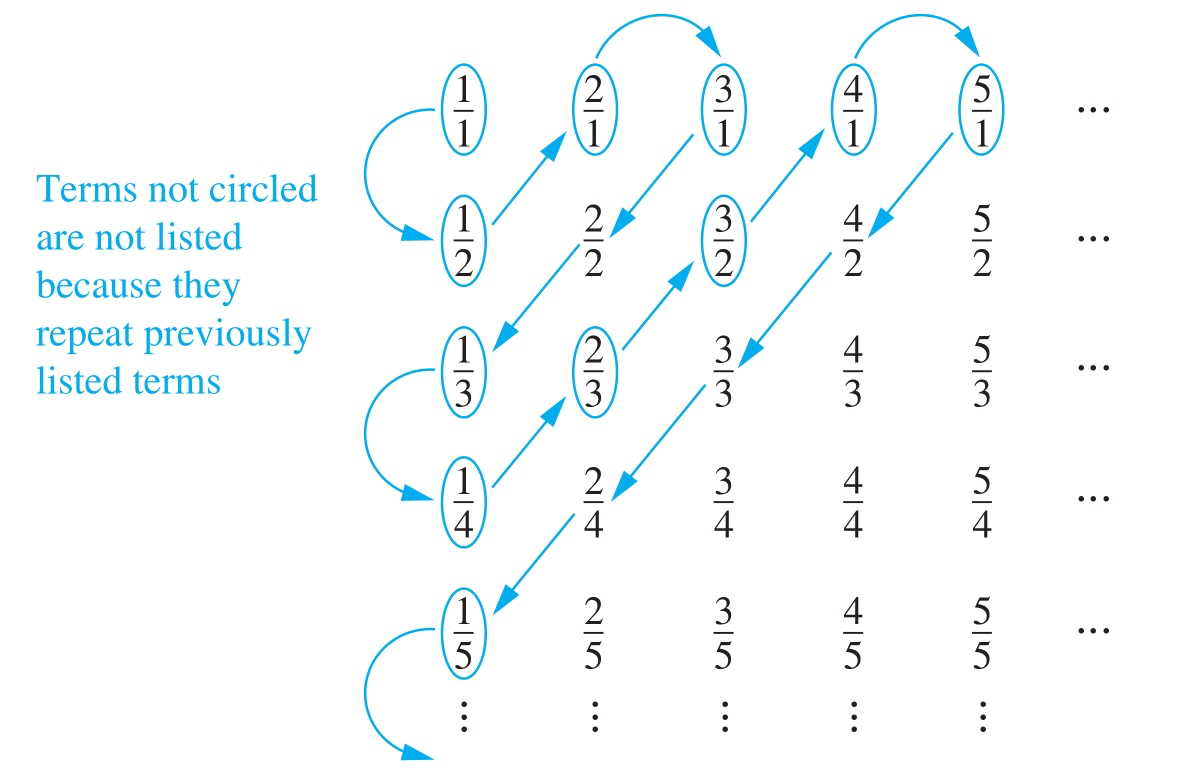
沿着途中箭头的方向,遍历有理数阵列,每个有理数的分子分母之和为k,在正整数集合M中必然有一个k与之对应,于是就建立了集合M和N之间的一一对应关系。
从直观上看,正整数集是有理数集的真子集,有理数集应当比正整数集大得多,但实际上并非如此,它们是一一对应的。
- 实数是不可数的
首先定义自然数是可数的,虽然自然数集合是一个无穷集合。根据前面的结论可知,有理数也是可数的,那么实数可数吗?
康托尔提出了著名的对角线方法,对此给出了证明:
考虑0到1之间的所有实数,假定它们是可数的,那么可以将该集合的数在序列P 中列出。每个 p_i 都可以被唯一地写作无限十进制小数,这样所有的实数序列就可以显示于以下阵列中:
那么我们总可以构造出一个实数b,
最关键的一步,令 不等于 (这里的 和矩阵的特征值异曲同工), 则b不在 P序列中。
但是,又因为b也是实数,按我们最初的定义,b又应该在 P序列中,从而导出矛盾。
从而说明我们的初始假设是错误的,实数是不可数的。
对角线方法看似简单,却是一个极其深刻和强大的方法,可以揭示出数学系统中内在关系的矛盾性,集合论中很多数学定理的证明依赖于对角线原理。
康托尔给这种不可数的实数集合取名为“连续统”,这一刻集合论诞生了,无穷集合之间,规模亦有不同。
整个数据的基础建立在了康托尔的集合论的基础之上,第二次数学危机带来的关于无穷小量的危机被解除了,数学家们对未来充满了信心。
数学基础的重建
很不幸,数学家们过于乐观了,集合论存在着阿喀琉斯之踵,即自我矛盾的性质——悖论。
康托尔在研究最大集合性质的时候,已经发现了悖论。基于对角线定理,容易证明一个无穷集合M的幂集,包含元素的数量大于M的元数数量。假设存在最大集合S,是一切集合的集合,那么 的幂集,包含元素数量大于S,可是由于已知S是最大集合,那么 的元数数量又不能大于S,由此导出矛盾。
罗素提出了一个通俗的理发师悖论:一个村里的理发师,宣称只帮不给自己刮胡子的人刮胡子,并且给所有这样的人刮胡子,请问这个理发师应该给自己刮胡子吗?[PS]我觉得还可以有一个更通俗的版本,再优秀的外科医生,也无法给自己做麻醉手术。
罗素悖论的主要问题是自我指涉,让逻辑推理陷入了恶性循环。注意这要和算法中的递归区分开来,递归有着有穷性的要求,不可陷入无限循环。
为了应对第三次数学危机,重建一个稳固的数学大厦,出现了四个流派,分别是逻辑主义、直觉主义、形式主义、公理集合论学派。
希尔伯特的形式主义
欧几里得几何的5条公设:
- 直线公设:从任意一点到另一任意一点,可以画一条直线。
- 线段延长公设:一条有限长线的线段可以无限地延长。
- 圆公设:以任意点为圆心,以任意的已知长度为半径,可以画一个圆。
- 直角公设:所有直角都相等。
- 平行公设:如果两条直线都与第三条直线相交,并且在同一侧的两个内角之和小于两个直角,那么这两条直线在这一侧相交。
第五条是著名的平行线公设,有一个等价版本:给定一条直线,通过此直线外的一点,有且只有一条直线与之平行。
千百年来无数的科学家前赴后继试图从前面4条公设推导出第五公设,但是无一成功。人们发现第五公设是独立存在的,这让数学家们的恐慌到达了顶点。如果第五公设没那么正确,那么欧式几何的基础就要被动摇了。
事实上,数学家们通过对第五公设的修改,罗氏几何、黎曼几何等非欧几何等曲面几何被创造出来,取得了丰硕的成果。非欧几何对于现实更有意义,因为现实世界中曲面比平面多得多,非欧几何也启发了后来爱因斯坦的广义相对论方程。
数学家们发现,公理不再是数学的起点,只要容许对公理系统作出不同的解释,找出不同的模型,那就有可能开辟一个新的领域(PS:凡诸有相,皆为虚妄)。非欧几何的创建,启发了数学家们的思想从实质公理化到形式公理化的过渡,为希尔伯特最终建立“形式化公理系统”奠定了基础。
希尔伯特形式化公理系统,是希尔伯特提出的数学系统构建范式,核心是将数学分支(代数、集合)转化为完全符号化,无意义依赖的形式,仅通过预设的机械法则推导出结论。演算是从无意义的符号出发的,而非依赖于逻辑公理。
在欧式几何的场景下,这些符号代表了点、线、面等概念,“过两点有且只有一条直线”这样的逻辑公理,被转化为相应的符号化语句。在整数计算领域,符号代表了自然数,加减乘除之类的运算规则,被转化为相应的符号化语句。
希尔伯特的形式化论证思想,他称之为”元数学“,又可被称为证明论,将研究对象,变成了”数学证明“本身,通过抽象的符合和机械法则,论证数学各个领域的命题。
形式化系统的核心目标,是要在有穷的步骤内,证明该系统的:
- 一致性:公理之间必须是相容的,不应推导出相互矛盾的结论。
- 完备性:通过已有的公理,可以推导出系统中所有的定理。
- 可判定性:存在算法判断任意符号命题是否为定理。
- 独立性:系统的公理之间是没有冗余的。
希尔伯特是形式主义的领军人物,希尔伯特提出建立公理化形式系统的证明论来解决数学危机。他接受了康托尔提出的实无穷,但要求在有穷的证明步骤里得出结论。
终结者哥德尔
正当希尔伯特对数学的未来充满信心时,哥德尔发现了不完备性定理,让形式化系统成为了泡影。哥德尔的发现,如洪钟大吕般震撼了整个20世纪的数学界,哥德尔不完备性定理对数学的贡献,好似爱因斯坦的相对论对于物理学的贡献。
哥德尔不完备性定理的核心结论可概括为两点:
- 第一定理(不完备性):在任何包含自然数算术的一致公理系统中,总存在至少一个既不能证明为真,也不能证明为假的命题(即不可判定命题)。
- 第二定理(一致性不可证):若一个包含自然数算术的公理系统是一致的,那么该系统的一致性无法在系统内部被证明。(需要额外的外部系统来证明)
可以通过”这句话无法被证明”这样的悖论来辅助理解,这个命题涉及到了逻辑自指:若它能被证明,则它为假命题,引发矛盾;若它无法被证明,则它为真,但是系统无法判断这个命题。
哥德尔不完备性定理,也深刻揭示了形式系统中的”可证“和”真“是两个概念。”可证“只涉及从公理出发的一系列演绎推理步骤是否严格,而”真“则涉及公理本身是否合理。这就将形式系统的语法和语义(或者说形式与内容)进行了明确的区分。
[PS]将形式和内容分开,是一种很有用的思维方式。比如一个线上故障,根因可能是编码或者架构问题(内容),也可能是流程问题甚至是组织架构问题(形式),举例来说,如果A团队系统的核心稳定性,依赖B团队提供的基础服务,但是在B团队该服务却是无人关心的边缘服务,那么故障是很难避免的。
哥德尔不完备定理,打破了“数学可以通过一套有限的公理系统,证明所有真理”的美梦,证明了数学的“完备性”和“一致性“无法同时实现。很遗憾,时至今日,数学并未如希尔伯特所愿,收敛到一个坚实稳固的基础。
不完备定理,也有其积极意义,如果真的可以靠一套符号系统,结合运算规则,就可以证明所有真理,那么人类的思考,就可以被计算完全取代,数学的发展就再也不需要人类的智慧了。
图灵的可计算数
图灵作为计算机领域的开山鼻祖,提出的图灵机模型,在抽象的数学世界和具体的物理世界之间,构建起一座智慧的桥梁。
按照图灵的定义,图灵机是一个非常简单的模型,它有一个控制器,一个读写头,同时有一个纸带。这个纸带是无限长的,上面排列着一个个格子,每个格子记录着一个符号。
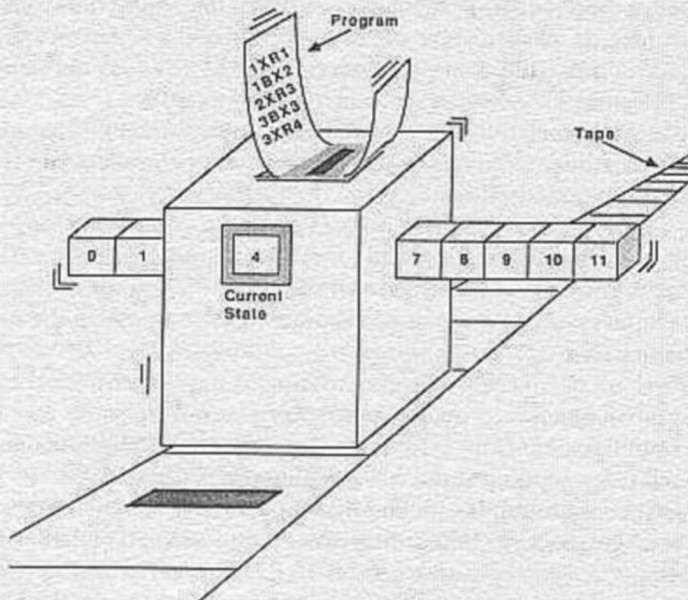
图灵机独特的伟大之处在于,将操作本身也通过编码实现了数字化,图灵机处理的都是数字,可以用一种极其简单的机械方式进行操作。[PS]在计算的世界里,程序和数据本质相同,都是数字,当代码化作二进制流,穿越CPU时,它们是平等的。
图灵观察到了数的一个新的性质:可计算性。能够通过有穷步骤算法获得准确结果的数,被称为可计算数。自然数和有理数是可计算数,这个比较显然,一些图灵机可以计算的超越数,比如PI、自然对数e、欧拉常数,也是可计算数,可以通过算法得出精确值。
判定性问题的证明
图灵判定性问题,更准确地说是“停机问题”(Halting Problem),是指“是否存在一个算法,能够判断任意一个计算机程序和它的输入最终会停止运行”。
判定性问题和哥德尔不完备性定理一脉相承。判定性问题研究是否存在一个通用的算法,可用于判定任意问题是否可证。
图灵证明判定性问题的核心步骤,是证明可计算数,是不可有效枚举的,存在可定义但是不可计算的数。图灵通过使用康托尔的对角线方法证明了这一点:
假设所有的可计算数,都可以有效枚举,那么列出所有的可计算出a的集合,
令:
这里我们使用的是二进制,每一位只有0和1。尝试构造一个数b ,令b 的每一位,都是a 对角线的翻转,即 如果b 是可计算的,那么b 一定包含在集合a中,所以一定存在一个数K,使得:
根据b 的定义,对n 有 ,令n=k,则有 , 1为偶数,得出矛盾。
因此,b是一个不可计算数,所以得证无法有效枚举所有可计算数。
图灵机是可执行的指令集,每一台图灵机都可以表达成一个可计算数,图灵接下来证明,不存在一台通用图灵机,可以判定一个给定数字,是否为一个非循环图灵机的描述数,大致的证明思路:
- 假设这样的通用图灵机H存在,它的作用是从1开始枚举所有正整数n,以检测一台图灵机的描述数是否为结构良好的非循环机。
- 这样的图灵机H是一个非循环图灵机,因为它总在有限步骤内终止并输出结果。
- 机器开始运行,所有的过程运行正常,直到图灵机H检测自己的描述数H’时,遇到了困境。为了检测H’,它必须再重头开始运行自己,于是周而复始陷入了死循环。这与图灵机H是非循环机相矛盾。
这里的证明和理发师悖论异曲同工。
图灵证明的是,不存在一个通用的机械方法,在有限步骤里可以判定一个命题是否可证。即图灵机如果不实际运行一遍,无法判断另一台图灵机的产出。
计算的极限
计算复杂性理论
哥德尔、图灵等人建立的可计算性理论,充分表明在自然数为基础的初等算术中,存在一些不可计算、不可判定的命题和函数。科学研究者们的兴趣,转向了哪些问题是可以计算的,需要多少步才能完成计算,这个领域又被称为计算复杂度。
多项式时间复杂度内可以完成计算的问题,被称为P问题,这类问题在输入规模较大时仍然能够高效运行。
有的问题,计算规模呈指数级增长,则被视为计算机不可计算的问题。
在多项式时间过程和指数时间过程之间存在着巨大的鸿沟,有一类问题,虽然也很难,但是计算机有可能求解,NP问题被定义出来。NP问题的全称是非确定性多项式时间过程,指的是能在多项式时间内,验证答案是否正确。
NP问题的特点是结果容易校验,但是求解过程可能很难。比如大数的质因数分解,是一个典型的NP问题。对于一个大数,找出所有的质因数,找不到高效的算法,但是如果给定一个质因数,可以在多项式时间内,很快验证是否为这个大数的因数,做一个除法就可以。
NP问题里面,最难的一部分问题,被称为NP完全(NPC)问题,所有的NP问题都可以“规约”到NP完全问题,只要解决了这类最难的问题,那么所有的NP问题就都解决了。
P/NP问题,很可能关乎人类思维能力的边界,P类问题是人们能够想明白的问题,NP问题可能是人们想破脑袋也想不明白的问题。
并行计算
对于P类问题,由于时间资源比较宝贵,人们很自然地考虑通过增加计算处理器资源,来缩短计算时间,即并行计算的模式。
向量化技术是在计算机硬件结构中完成并行化的核心技术,关键是SIMD(Single Instruction, Multiple Data), 即通过一条指令同时操作多条数据。将多条指令合并成一条指令的过程就是向量化。
今天的GPU(Graphic Processing Unit)是并行计算加速硬件的助力。NVIDIA公的GPU没有向量硬件,通过SIMT(单指令多线程)的线程束来模拟实现向量硬件。
GPU和CPU的主要区别,在于GPU将结构中较大比例的晶体管用于运算单元,而仅有极少比例的控制单元和缓存单元,因此GPU的逻辑运算能力相对较弱,但擅长并行处理无依赖关系的简单任务。
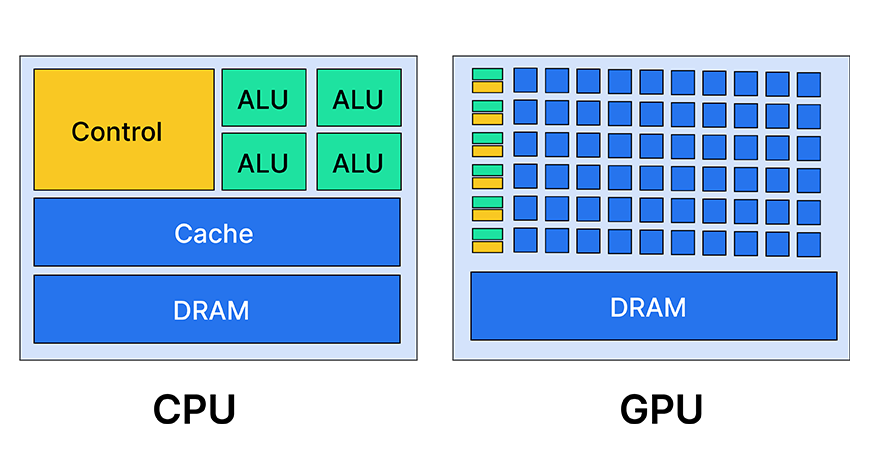
并行计算的一个子集是分布式计算,好的分布式计算需要有“数据并行化”和“任务并行化”设计。分布式计算发展出了云计算形态,将大规模服务器集群当成一台计算机来使用。很对高并发负载或者突发性的大量请求,集群的计算能力可以实现弹性扩缩容。
量子计算
现在的经典计算机,核心元件是晶体管,即所谓的硅基。晶体管是一种半导体,在同步电压下控制电子的流通,来表示0和1的状态。
量子计算依赖的物理基础更加底层,即量子比特。量子的概念涵盖目前标准模型中所有的61种微观粒子,比如电子、光子、夸克等。作为事物不可分的最小单位,量子是离散的而非连续的。量子理论主要采用的数学工具是线性代数。
经典计算的比特是一个信息单位,每一个比特有确定的状态,要么是0,要么是1,8个比特组成1字节(Byte)。与经典计算的比特不同,量子比特可以是1和0的叠加态,可以既是0又是1(违反人类直觉但却是量子比特物理性质),那么8个量子比特,就可以同时表示 2^8 种状态。
可以使用通信领域的多路复用来类比理解,通过共享物理信道,同时传递多路信号。量子比特通过叠加态,实现并行计算。
以抛硬币距离,同时抛30枚硬币,一共有2^30种可能状态,需要大约10亿个数字去表示。但是如果用量子比特来表示的话,只需要30个量子比特就可以并行计算所有的可能性,极大提升了计算效率。
量子计算,离现实落地还比较遥远,一个原因是制造量子计算机面临巨大困难,另一个原因是需要寻找适用量子计算场景的量子算法。
复杂性计算
计算机作为人类探索自然最重要的工具之一,可以帮助人们对各种自然现象进行建模、模拟和预测,同时,计算机背后的计算理论,也可以用来解释很多的自然系统,为人类认知自然提供了一种全新的视角,计算机和计算理论,启发促成了现代复杂性科学的萌芽,包括控制论、系统论、人工智能、自适应系统、计算动力学、计算生物学等前沿学科。
在复杂系统中,系统内部的元素之间、系统与环境之间,会频繁发生相互作用,我们无法通过观察所有微观元素,来把握系统的整体走向。
经典科学的内核 —— “还原论”,认为系统可以被不断拆分成组成元素,系统的整体行为可以通过局部元素的行为来解释,然而还原论思想在复杂系统面前苍白无力,一只蚂蚁的爬行路径很难解释整个蚁群行进的路线,上千只蚂蚁互相发生交流和影响才决定了蚁群的整体前进方向,复杂系统具有“可分解但不可还原”的特点,逆向计算的难度远远大于正向计算。
复杂性的简单算法
对于计算机科学家来说,算法的功能和现象有可能来自简单规则的重复迭代,这启示我们可以通过递归算法来处理复杂系统。算法的迭代性和有穷性,让简单算法生成复杂结果变得可能。尤其是如果在算法中加入了随机信息,以及引发了一些非线性运算,则有可能引起全局性的性质改变,我们称其为涌现。
涌现在生物学中被称为进化,在物理学中被称为相变,在市场营销中被称为引爆。如果说分析是对事物的一种分解,是一个将整体分解为局部,将复杂还原为简单的过程,那么涌现就是其逆运算,恰好完成了从低层次到高层次的飞跃,实现了从简单到复杂的突变。
网络科学
- 小世界网络
生物神经网络、人类社会网络均是典型的小世界网络。节点之间的平均路径较短,从网络的某一点出发,可以快速到达远端的任意另一点,短直径让它能够对外部环境的刺激做出迅速反应,因此有着高度的适应性。稀疏、高聚类是小世界网络的特点,它是最平衡的网络。
- 无标度网络
互联网、铁路网组成的网络被称为无标度网络,网络中节点的链接数量服从幂率分布,会出现一些头部的超级节点,这些节点拥有最多的连接链路。
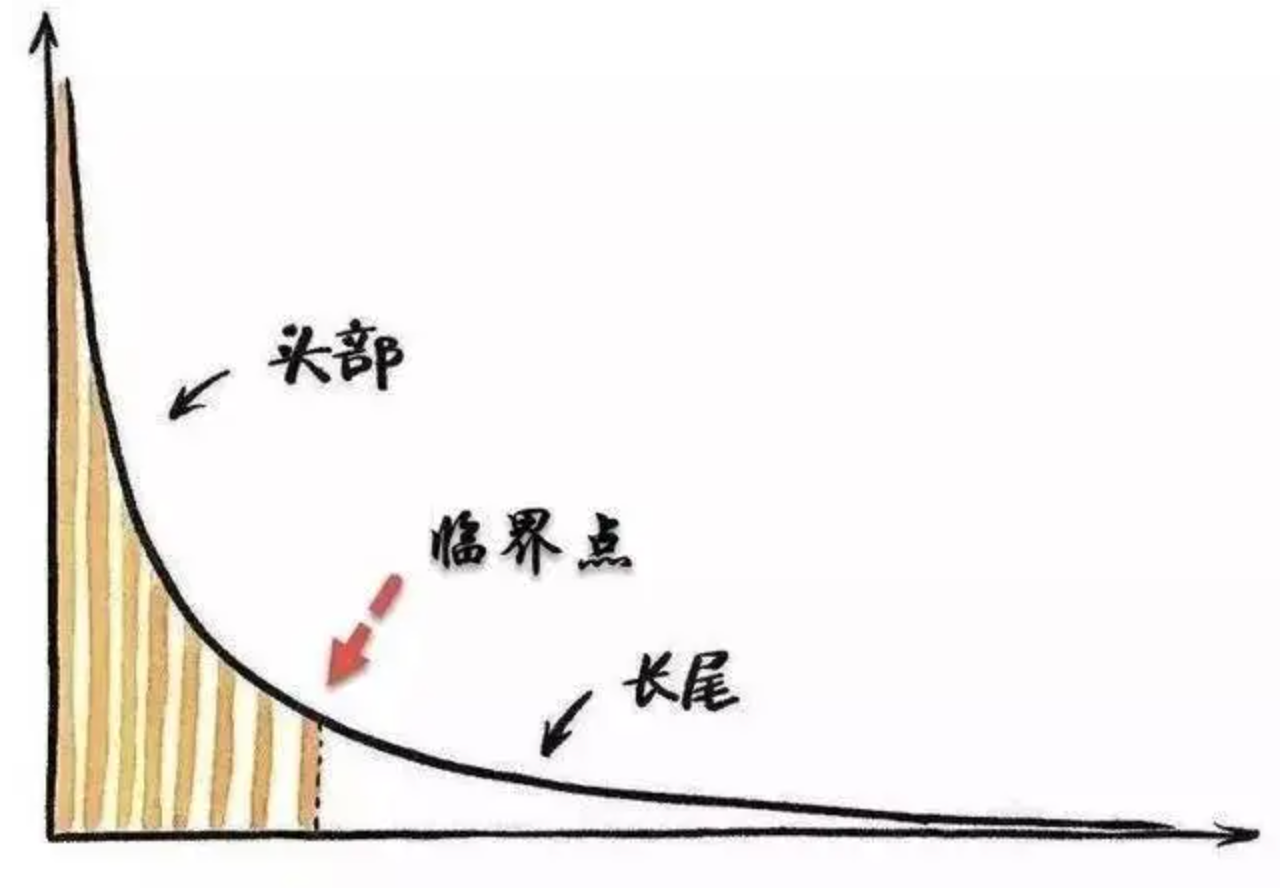
因此在互联网中,存在着70-20-10定律,也就是一个领域的巨头往往涌现成为hub节点,占据70%的市场份额,第二名占据20%,剩下的是长尾。无标度网络的另一个特点是网络结构较为健壮,对随机攻击有很好的抗击能力,因为随机攻击大概率会落在长尾节点。
机器能思考吗
大脑是由神经元之间的相互连接和作用完成计算的,人类智能是由大量神经元非线性地处理信息后所涌现的结构。
由于构造机制的不同,机器不会按照和人类完全一致的方式去完成思考。
但是如果从实际产生效果的角度去看,如图灵测试所论述的那样,那么机器是可以有智能的。
图灵在1950年著名论文《机器机器与智能》中明确提出了”机器能思考吗“这一问题,通过一种回答问题的模仿游戏来对比人和机器的智能,即图灵测试。[PS]时至今日,一个普通人类和一个AI大模型一起去参与图灵测试,来一场实况PK的话,大概率是AI大模型胜出。
算力和推理的互相转化
计算机的价值,不仅仅在于帮助人类执行大量的、重复的运算,而是正在逐渐代替人类参与高级计算活动,当今的计算机正在逐步接管人脑的感知、推理、分析和决策能力。
[PS]辅导小学生解数学难题的时候,家长们经常发现,如果引入方程,很多难题就会变得特别简单,这本质就是在把复杂的逻辑推理,转换成了简单计算。
今天的程序设计,都非常强调对机器的友好性,便于让机器高效执行,要求程序员具备“面向机器的计算思维(computational thinking)”。程序员需要很好地理解,计算机能够做哪些事情,擅长做哪些事情。如何将小数据、小计算量下的难问题,转换成一个大数据、大计算量下的简单问题,考验着程序员们定义问题的能力。人们需要相信,在一个好的设计下,机器大脑会比人类大脑更聪明,能更高效地解决问题。
2016年,DeepMind的机器智能产品AlphaGo首次击败了围棋世界冠军李世乭,这被看做是AI发展史的标志性里程碑。在这之后,AlphaGo通过和自己对弈,不断迭代发展,人类在围棋领域已经被AI甩开很远,再也无法求得一胜。今天的围棋选手,如果要有境界上的突破,更多地需要向AI学习下棋的思路。
[PS]通常人们会把这个事件看做AI对人类的胜利,但我觉得也可以看成人类和AI一次成功的合作:人类通过智慧发明了围棋,制定了精妙的规则,计算机通过算法和算力,在该领域拓展了人类智力的边界。
以ChatGPT为代表的大语言模型(LLM, Large Language Model),开启了AI架构的全新范式。大模型的思路是特别的,首先它使用的训练模式是基于全量、全局的数据进行的,使用全局数据内在的统计概率来替代语法和句法,最后实现代替语义;其次Promoting的模式去除了模型对数据的依赖,借助大模型已有的全局数据内在统计概率,生成任何内容。
会使用工具不再是人类的专利,机器通过学习使用工具快速缩小和人类的差距。AI agent之间可以相互交互,形成复杂的agent网络,通过协作完成复杂的任务。
大模型提升了知识工作者的效率,在大模型时代,人的经验、态度和想象力才是最有价值的,死记硬背越来越没有必要。我们极有可能经历人类近8000年文明史上从未出现过的一幕,大多数人不需要每天工作,但社会的财富总量却在增加,因为机器在不断生产和创造财富。
借助计算机的强大算力,年轻的数学家们获得了一种新的工作方式,通过个例给出猜测,然后设计实验让计算机模拟,快速验证猜测的结论。这可能打破了过去2000多年来的数学研究范式:基于公式和推理的逻辑演绎。
[PS]要获得这项面向未来的先进能力,人类需要作出很多的观念转变:
- 放下比较心态,人类如果要和AI一争高下,起心动念就错了,选错了对手。AI没有失败的成本,在机器擅长的领域,人类没有任何胜算,所以和AI竞争是没有出路的。
- 放下傲慢,接纳机器作为人类能力的延伸,同时培养自身的计算思维,采取更开放积极的心态,学会和机器合作。
- 放下恐惧,如果一直陷于被机器取代的恐惧之中而止步不前,反而最后一定会被机器取代。人类是AI的创造者,但是不必比AI更聪明。最好的策略是和AI做朋友,积极拥抱AI技术,利用AI的能力提升工作生活的效率。
一种计算主义的世界观
计算主义者相信丘奇——图灵论题的心灵版本,相信大脑是一台计算机,人的心智由这台计算机运行而来。
如果大脑是一台图灵机,那么它必然是不完备的,也就是说存在一些大脑无法计算的问题。已知的一个最著名的不可计算问题,就是模拟自身的判定性问题,即图灵停机问题,对应的人生版本,即“我是谁”这个问题,[PS]这类问题很容易让人陷入内耗,不要自证,“不要回答”。
同样地,如果大脑是一台图灵机,那么它也无法判定另一台图灵机是否会停机。对应的人生版本,不要介入别人的因果,同时也没有谁可以决定你的命运,不存在一个事先已存在的宿命的终点,认真生活之后方能知道未来的结果。
那么命运和什么有关呢?从计算主义的观点来看,和时间资源、算力资源有关。生命过程中的进化计算有两种,首先是生命本身的进化,积累出了生存需要的生理功能;其次是大脑的神经网络在成长过程中的进化,积累出了认知和思维。这两种进化都需要时间的积累,才能涌现出所需的功能结构,所以时间是宝贵的。人要形成智慧,取决于大脑的神经网络对记忆和知识的综合调动能力,从而达到洞察、创新的目的。
聪明和智慧是两件事情,聪明的人智商高,但只是脑子转得快,这主要取决于大脑营养够不够。聪明不能决定智慧,智慧取决于大脑的神经网络对记忆和知识的综合调动能力,从而达到洞察、创新的目的。
尾声
道哥写这本书,光附录中就列了93本参考书籍,买遍了市面上能买到的计算机书籍,家中因此多了一座图书馆,最终写就了这部详实又深刻的《计算》。
在大模型计算引领浪潮的AI时代,大模型中近乎包含了人类已有的所有知识,然而,正如抱着一本字典,不能说自己通晓所有汉字,对牛顿三定律倒背如流,并不能让你成为牛顿,熟练使用AI大模型,无法代表对世间知识尽在掌握。掌握知识的幻觉,反而会阻塞真正求知的道路。真正的求知之路,一定离不开深入探索,反复参悟,思考内化。
在书中除了计算知识的介绍,道哥也叙述了很多大师们的轶事生平,不仅增加了本书的趣味性,也为本书增添了人文主义光辉。技术人不要陷入狭隘的技术主义。技术的高低,不是度量世界的唯一标尺,对世界的热爱程度,决定了人生的高度。
计算,为了无法计算的价值。